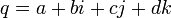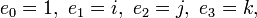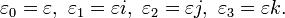• Mathematician Wilhelm Karl Joseph Killing, 1847
• Mathematician Eduard Study, 1862
• Mathematician Issai Schur, 1875

Wilhelm Karl Joseph Killing (May 10, 1847 – February 11, 1923) was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non - Euclidean geometry.

Killing studied at the University of Münster and later wrote his dissertation under Karl Weierstrass and Ernst Kummer at Berlin in 1872. He taught in gymnasia (secondary schools) from 1868 to 1872. He became a professor at the seminary college Collegium Hosianum in Braunsberg (now Braniewo). He took holy orders in order to take his teaching position. He became rector of the college and chair of the town council. As a professor and administrator Killing was widely liked and respected. Finally, in 1892 he became professor at the University of Münster. Killing and his spouse had entered the Third Order of Franciscans in 1886.

In 1878 Killing wrote on space forms in Crelle's Journal 86:72–83. Two years later he wrote on computations in hyperbolic geometry in the same journal. Recounting lectures of Weierstrass, he there introduced the hyperboloid model described by Weierstrass coordinates.

Killing invented Lie algebras independently of Sophus Lie around 1880. Killing's university library did not contain the Scandinavian journal in which Lie's article appeared. (Lie later was scornful of Killing, perhaps out of competitive spirit and claimed that all that was valid had already been proven by Lie and all that was invalid was added by Killing.) In fact Killing's work was less rigorous logically than Lie's, but Killing had much grander goals in terms of classification of groups, and made a number of unproven conjectures that turned out to be true. Because Killing's goals were so high, he was excessively modest about his own achievement.

From 1888 to 1890, Killing essentially classified the complex finite dimensional simple Lie algebras, inventing the notions of a Cartan subalgebra and the Cartan matrix. Élie Cartan's dissertation was essentially a rigorous rewriting of Killing's paper. Killing also introduced the notion of a root system. He discovered the exceptional Lie algebra g₂ in 1887; his root system classification showed up all the exceptional cases, but concrete constructions came later.

As A. J. Coleman says, "He exhibited the characteristic equation of the Weyl group when Weyl was 3 years old and listed the orders of the Coxeter transformation 19 years before Coxeter was born."

Eduard Study (March 23, 1862 – January 6, 1930) was a German mathematician known for work on invariant theory of ternary forms (1889) and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.

Study was born in Coburg in the Duchy of Saxe - Coburg - Gotha. He died in Bonn.

Eduard Study began his university career in Jena, Strasbourg, Leipzig and Munich. He loved to study biology, especially entomology. He was awarded the doctorate in mathematics at the University of Munich in 1884. Paul Gordan, an expert in invariant theory was at Leipzig, and Study returned there as Privatdozent. In 1888 he moved to Marburg and in 1893 embarked on a speaking tour in the U.S.A. He appeared at the primordial International Congress of Mathematicians in Chicago as part of the World's Columbian Exposition and took part in mathematics at Johns Hopkins University. Back in Germany, in 1894, he was appointed extraordinary professor at Göttingen. Then he gained the rank of full professor in 1897 at Greifswald. In 1904 he was called to the University of Bonn as the position held by Rudolf Lipschitz was vacant. There he settled until retirement in 1927.

In 1891 Eduard Study published “Of Motions and Translations, in two parts”. It treats Euclidean space through the space group. The second part of his article constructs a seven - dimensional space out of “dual biquaternions”, that is numbers

where a, b, c, and d are dual numbers and {1, i, j, k} multiply as in the quaternion group. He uses these conventions:

The multiplication table is found on page 520 of volume 39 (1891) in Mathematische Annalen under the title “Von Bewegungen und Umlegungen, I. und II. Abhandlungen”. Eduard Study cites William Kingdon Clifford as an earlier source on these biquaternions. In 1901 Study published Geometrie der Dynamen to highlight the applications of this algebra. Due to Eduard Study’s profound and early exploitation of this eight - dimensional associative algebra, it is frequently referred to as Study Biquaternions. Study’s achievement is celebrated, for example, in A History of Algebra (1985) by B. L. van der Waerden, who also cites Clifford’s earlier note.

Since the space group is important in robotics, the Study biquaternions are a technical tool, now sometimes referred to as dual quaternions.

In 1898 Eduard Study was the author of an article on hypercomplex numbers in the Klein's encyclopedia. This 34 page article was expanded to 138 pages in 1908 by Élie Cartan, who surveyed the hypercomplex systems in Encyclopédie des sciences mathématiques pures et appliqueés. Cartan acknowledged Eduard Study’s priority in his title with the words "after Eduard Study".

In the 1993 biography of Cartan by Akivis and Rosenfeld, one reads:

[Study] defined the algebra °H of ‘semiquaternions’ with the units 1, i, ε, η having the properties

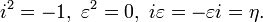
Semiquaternions are often called ‘Study’s quaternions’.

In 1985 Helmut Karzel and Günter Kist developed "Study's quaternions" as the kinematic algebra corresponding to the group of motions of the Euclidean plane. These quaternions arise in "Kinematic algebras and their geometries" alongside ordinary quaternions and the ring of 2 × 2 real matrices which Karzel and Kist cast as the kinematic algebras of the elliptic plane and hyperbolic plane respectively.

Thus in the study of classical associative algebras over R there are two special ones: Study’s quaternions (4D) and Study’s biquaternions (8D).

Study's work with dual numbers and line coordinates was noted by Heinrich Guggenheimer in 1963 in his book Differential Geometry. He cites and proves the following theorem of Study: The oriented lines in R³ are in one-to-one correspondence with the points of the dual unit sphere in D³. Later he says "A differentiable curve A(u) on the dual unit sphere, depending on a real parameter u, represents a differentiable family of straight lines in R³: a ruled surface. The lines A(u) are the generators or rulings of the surface." Guggenheimer also shows the representation of the Euclidean motions in R³ by orthogonal dual matrices.

In 1905 Study wrote "Kürzeste Weg im complexen Gebiet" (Shortest path in complex domains) for Mathematische Annalen (60:321–378). Some of its contents were anticipated by Guido Fubini a year before. The distance Study refers to is a Hermitian form on complex projective space. Since then this metric has been called the Fubini – Study metric. Study was careful in 1905 to distinguish the hyperbolic and elliptic cases in Hermitian geometry.

Somewhat surprisingly Eduard Study is known by practitioners of quantum chemistry. Like James Joseph Sylvester, Paul Gordan believed that invariant theory could contribute to the understanding of chemical valence. In 1900 Gordan and his student G. Alexejeff contributed an article on an analogy between the coupling problem for angular momenta and their work on invariant theory to the Zeitschrift für Physikalische Chemie. In 2006 Wormer and Paldus summarized Study's role as follows:

The analogy, lacking a physical basis at the time, was criticized heavily by the mathematician E. Study and ignored completely by the chemistry community of the 1890's. After the advent of quantum mechanics it became clear, however, that chemical valences arise from electron - spin couplings ... and that electron spin functions are, in fact, binary forms of the type studied by Gordan and Clebsch.

Issai Schur (January 10, 1875 in Mogilev – January 10, 1941 in Tel Aviv) was a mathematician who worked in Germany for most of his life. He studied at Berlin. He obtained his doctorate in 1901, became lecturer in 1903 and, after a stay at Bonn, professor in 1919.

He considered himself German rather than Jewish, even though he had been born in the Russian Empire in what is now Belarus, and brought up partly in Latvia. For this reason he declined invitations to leave Germany for the United States and Britain in 1934. Nevertheless he was dismissed from his chair in 1935 and, at the instigation of Ludwig Bieberbach (who had previously sympathized with Schur regarding his treatment at the hands of the Nazis), he was forced to resign from the Prussian Academy in 1938. Schur eventually emigrated to Palestine in 1939, and lived his final years in poverty. He died in Tel Aviv on his 66th birthday.

As a student of Frobenius, he worked on group representations (the subject with which he is most closely associated), but also in combinatorics and number theory and even theoretical physics. He is perhaps best known today for his result on the existence of the Schur decomposition and for his work on group representations (Schur's lemma).

Schur had a number of students, including Richard Brauer, B.H. Neumann, Heinz Prüfer, and Richard Rado. His lectures were very popular with students. He was elected to the Academy of Sciences of the USSR as a foreign corresponding member in 1929.

Schur published under the name of both I. Schur, and J. Schur, the latter especially in Journal für die reine und angewandte Mathematik. This has led to some confusion.